A New Upper Bound for the Moving Sofa Problem

The moving sofa problem is a fairly well-known open problem that essentially asks: “What is the largest area of a shape that can pass through a unit width corridor with an L shape?”

Fairly complex sofa constructions have been offered for this problem. Notably, Joseph Gerver presented a sofa with an area of 2.2195 [1], and Philip Gibbs computationally found a sofa with a seemingly identical shape [2]. However, no rigorous proof has been offered for the optimality of this sofa shape to this day. The oldest upper bound for the sofa area was 2.8384, by Hammersley [3] (as a problem in an interesting text). In 2017, Yoav Kaullus and Dan Romik presented an approach with which they were able to rigorously certify that the sofa constant has an upper bound of 2.37 [4].

Through a ~2784 hour (~4 months) computation with a 3.10GHz Intel Xeon E3-1220 V2 CPU, I have been able to improve the upper bound to 273312688320182793625662961/116181097674087333888000000 = 2.352471. Raw data on the computation is available at https://github.com/mkturkcan/MovingSofaProblemBounds.

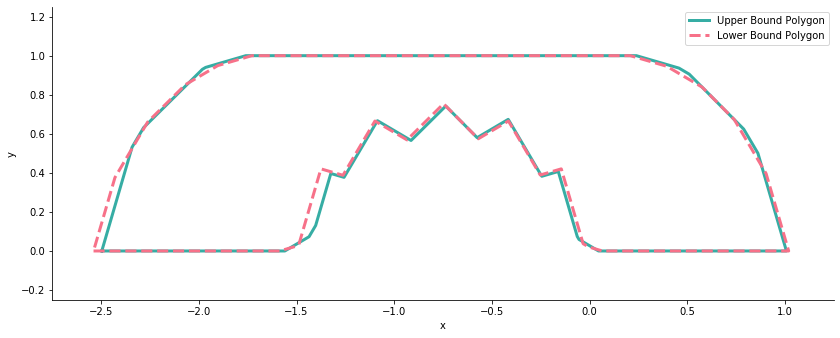
The upper bound polygon (as well as the lower bound polygon with area 160678044438594131134990137/68848057880940642304000000 = 2.333806) are shown below:

References:

[1] Gerver, Joseph L. “On moving a sofa around a corner.” Geometriae Dedicata 42.3 (1992): 267-283.

[2] Gibbs, Philip. “A Computational Study of Sofas and Cars.” Preprint available from World Wide Web (http://vixra.org/pdf/1411.0038v2.pdf) (2014).

[3] Hammersley, J. H. “On the enfeeblement of mathematical skills by ‘modern mathematics’ and by similar soft intellectual trash in schools and universities.” Bulletin of the Institute of Mathematics and its Applications 4, 1 22 (1968).

[4] Kallus, Yoav, and Dan Romik. “Improved upper bounds in the moving sofa problem.” Advances in Mathematics 340 (2018): 960-982.